Amar Benmahammed, Hind Nouar, Leila Haddad, Zahra Laala, Oulmi Abdelmalek & Hamenna Bouzerzour

Analyse de la stabilité des performances de rendement du blé dur (Triticum durum Desf.) sous conditions semi-arides

Document(s) associé(s)

Annexes

• pdf (892k)

Résumé

L'analyse des essais pluriannuels pour l'évaluation et la recommandation des variétés est une étape très importante en amélioration des plantes. Cette analyse porte sur le potentiel et la stabilité des performances génotypiques. La présente contribution compare quelques méthodes d'analyse de la stabilité des performances de 15 génotypes de blé dur évalués au cours de six campagnes agricoles sous conditions semi-arides. Les résultats indiquent des différences significatives de rendement entre génotypes et un changement de classement des performances génotypiques selon l'année, suggestives de la présence d'une interaction génotype x année. L'étude comparative des méthodes d'analyse de la stabilité groupe les indices de stabilité en deux ensembles, représentant la stabilité agronomique (P_i, Bot, S_rang, S_i⁽²⁾, S_i⁽³⁾, b_i) et la stabilité biologique (W_i et S²_di). Le premier groupe associe performance et stabilité et identifie deux génotypes stables et performants : Cyrus₁ et Heider/Martes//Huevos de Oro. Par contre, le second groupe n'informe que sur la stabilité et identifie Belikh₂ et Mrb₁₆/Ente//Mario comme étant les génotypes les plus stables. Ces résultats suggèrent l'utilisation des indices du premier groupe pour améliorer simultanément la stabilité et la performance de rendement. Cependant, dans le cas où la stabilité prime au détriment de la performance, il est conseillé d'utiliser les indices du second groupe.

Abstract

Stability analysis of yield performances of durum wheat (Triticum durum Desf.) under semi-arid conditions. Analysis of multi-seasons trials to evaluate and recommend varieties is an important step in plant breeding programs. This analysis focuses on both genotypic stability and performances. This contribution compares several approaches to measure yield stability using yield data of 15 durum wheat genotypes evaluated during six years under semi-arid conditions. The results showed significant yield differences among entries and a change of the genotypic rank across years, suggesting the presence of the genotype x year interaction. The stability approaches were grouped into two groups, representing agronomic concept of stability (P_i, Bot, S_rang, S_i⁽²⁾, S_i⁽³⁾, b_i) and biological concept of stability (W_i and S²_di). The first group combines information on yield potential and stability and identifies two stable and high yielding genotypes: Cyrus₁ and Heider/Martes//Huevos de Oro. While the second group focuses only on stability and showed that Belikh₂ and Mrb₁₆/Ente//Mario were the most stable genotypes. These results suggest the use of the indices of the first group to improve both stability and yield potential. However, in cases where stability is of paramount, it is advisable to use the statistics of the second group.

Table des matières

1. Introduction

1Sur les hauts plateaux algériens, les performances de rendement de la culture du blé dur (Triticum durum Desf.) sont limitées par l'action des stress de nature abiotique. La variation des rendements, d'une année à l'autre et d'un lieu à l'autre, a pour origine la sensibilité du matériel végétal à l'effet combiné des basses températures hivernales, du gel printanier, du stress hydrique et des hautes températures de fin de cycle de la culture (Bahlouli et al., 2005 ; Chennafi et al., 2006). La variation des performances génotypiques engendre l'interaction génotype x année, rendant difficile la sélection et la recommandation des génotypes performants (Bouzerzour et al., 1995).

2En présence d'interaction de nature qualitative, les sélectionneurs sont à la recherche de méthodes pour exploiter l'interaction dans le processus de sélection. La sélection pour l'adaptation spécifique est un moyen d'exploiter l'interaction (Annicchiarico et al., 2005). Le recours à l'étude de la stabilité des performances est un autre moyen qui permet de classer les génotypes selon leurs degrés de stabilité et de performance. De nombreuses méthodes d'analyse de la stabilité sont proposées dans la littérature (Lin et al., 1986 ; Becker et al., 1988 ; Sabaghnia et al., 2006 ; Rose et al., 2008). L'objet de la présente contribution est d'analyser la stabilité du rendement des variétés de blé dur (T. durum) évaluées sous conditions semi-arides.

2. Matériel et méthodes

2.1. Conduite de l'expérimentation

3Un essai a été mis en place sur le site de la station expérimentale de l'ITGC (Institut Technique des Grandes Cultures) de Sétif (Algérie), au cours des campagnes agricoles 2000-2001 à 2005-2006. Le matériel végétal est constitué de 15 génotypes de blé dur (T. durum) provenant de sélections locales et d'introductions de l'ICARDA (International Center of Agricultural Research in Dry Areas) et d'Europe. Ces génotypes ont été semés dans un dispositif en blocs avec trois répétitions, sur des parcelles élémentaires de 5 m de long par 1,2 m de large. La densité de semis adoptée est de 250 graines par m². L'essai a été fertilisé avec 100 kg^.ha^-1 d'engrais phosphaté à 46 % avant le semis et avec 100 kg^.ha^-1 d'engrais azoté (urée à 35 %) au stade tallage. Le contrôle des mauvaises herbes est fait chimiquement avec du GranStar (Tribenuron Methyl) à raison de 12 g^.ha^-1.

4Les notations ont porté sur la détermination de la durée de la phase végétative, notée en jours calendaires de la levée à la date d'épiaison ; la hauteur de la végétation, mesurée en cm au stade maturité ; les composantes du rendement grain ont été déterminées à partir de la végétation provenant de la fauche d'un segment de rang long de 1 m. Le rendement grain est mesuré suite à la récolte mécanique de l'essai.

2.2. Analyses des données

5L'analyse de la variance du rendement grain est réalisée par essai pour identifier les meilleurs génotypes par année et sur l'ensemble des années pour tester la présence de l'interaction génotype x année. L'analyse de la stabilité est approchée par le calcul de l'écovalence de Wricke (1962), l'indice de la supériorité génotypique de Lin et al. (1988a), la régression conjointe de Finlay et al. (1963), les indices de stabilité S_i⁽²⁾ et S_i⁽³⁾ de Nassar et al. (1987), la somme des classements (S_rang) des rendements de Kang et al. (1991) et les statistiques non paramétriques de stabilité de Fox et al. (1990).

6L'écovalence est calculée par :

7W_i = ∑(Y_ij - Y_i. - Y_.j + Y_..)²

8où W_i = écovalence du génotype i, Y_ij = valeur du génotype i de l'année j, Y_i. = effet moyen du génotype i, Y_.j = effet moyen de l'année j et Y_.. = moyenne générale de l'ensemble des génotypes et des années.

9L'indice P de Lin et al. (1988a) est calculé comme suit :

10P_i = [∑(Y_ij - M_j)]²/2n

11où Y_ij = rendement du génotype i de l'année j, M_j = rendement du génotype le plus performant de l'année j, n = nombre d'années testées.

12Dans la méthode de la régression conjointe, le rendement du génotype est régressé sur l'indice du milieu I_j (I_j = Y_.j - Y_..) pour générer deux statistiques : le coefficient de régression b, spécifique à chaque génotype évalué et le carré moyen des écarts résiduels de la régression (S^²_di). La déviation de l'unité du coefficient de régression est testée par rapport à l'écart-type du b. S²_di est testée par rapport à l'erreur résiduelle de l'analyse de la variance combinée (Annicchiarico, 2002).

13Les indices S_i⁽²⁾ et S_i⁽³⁾ de stabilité de Nassar et al. (1987) ont été calculés en utilisant les formules suivantes :

14S_i⁽²⁾ = ∑(r_ij - r_i.)²/(n-1) et S_i⁽³⁾ = ∑(r_ij - r_i.)²/r_i.

15où r_ij = classement du rendement du génotype i au cours de l'année j, r_i. = moyenne des classements du génotype i sur l'ensemble des années et n = nombre d'années.

16La stabilité a été aussi approchée par la méthode de la somme des classements (S_rank) des rendements (Kang et al., 1991). Dans cette méthode, les rendements de l'année j sont classés par ordre décroissant, le génotype dont le rendement est maximal prend le classement 1. Les valeurs de la variance de Shukla (1972) sont classées par ordre croissant. Le rang 1 est donné au génotype ayant la plus faible variance. S_rank est égale à la somme des rangs des rendements et de la variance (Kang et al., 1991 ; Rose et al., 2008). La variance (σ²_i) de Shukla (1972) a été calculée par :

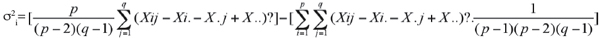
17avec p et q étant le nombre de génotypes et de campagnes. Les statistiques non paramétriques de Fox et al. (1990) sont déduites du classement des performances génotypiques par année et sur l'ensemble des années. Les génotypes dont le classement est situé dans le premier tiers (classement de 1 à 5) sont les meilleurs (TOP), ceux dont le classement est situé dans le tiers médian (classement de 6 à 10) sont moyens (MID) et ceux formant le dernier tiers (classement de 11 à 15) sont médiocres (BOT). Les logiciels CropStat 7.2 (2008) et OpenStat (Miller, 2007) ont été utilisés pour les différentes analyses statistiques.

3. Résultats et discussion

3.1. Variabilité génotypique du rendement grain

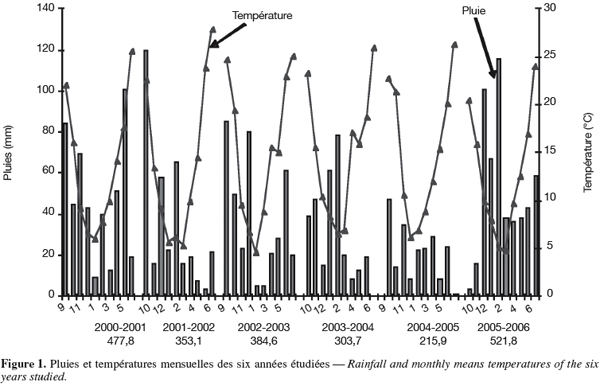
18La pluviométrie enregistrée au cours des différentes années montre une importante variation intra et inter annuelle. Le cumul pluviométrique varie de 215,9 à 521,8 mm. La répartition est relativement plus homogène en 2005-2006. Elle est, par contre, très irrégulière au cours des cinq autres années. Le régime thermique se caractérise par une allure bimodale, froid intense en hiver et températures élevées en fin de cycle de la culture (Figure 1). La moyenne des rendements grains de l'ensemble des génotypes varie 1,8 à 3,33 t^.ha^-1.

19L'analyse de la variance du rendement, par année, indique un effet génotype significatif, suggérant que des différences de performances existent entre les variétés testées. Cette analyse indique aussi que chaque année classe différemment les génotypes et notamment ceux qui présentent les meilleurs rendements grains. Ainsi au cours de 2000-2001, sept génotypes prennent la tête du classement : Adamillo/Duillo//Semito, Massara₁, Mrb₅, Cyprus₁, Waha, Mrb₁₆/Ente//Mario et Daki. Par contre, en 2001-2002, seul Mrb₅ est le meilleur et en 2002-2003, c'est la variété Deraa qui se classe première. En 2004-2005, c'est le génotype Cyprus₁ qui est en tête du classement (Tableau 1).

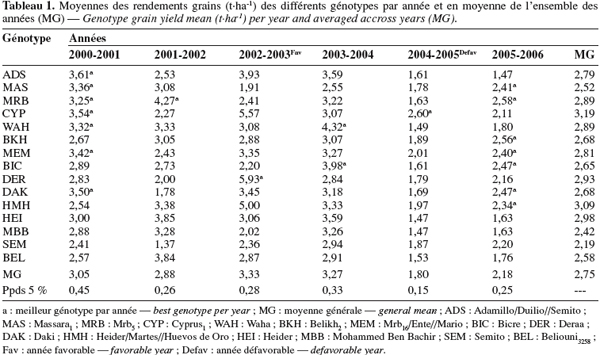
20Selon Yan et al. (2000), le changement du classement des génotypes d'une année à l'autre est une indication de la présence de l'interaction. On note cependant que, quelle que soit l'année, MBB, Beliouni, Semito et Heider se classent toujours en dernière position (Tableau 1). Ceci est une indication de leur faible potentiel de rendement grain. L'analyse de la variance combinée confirme la présence de l'interaction (test FGxE = 39,36**, P < 0,01). La présence d'une interaction significative suggère d'analyser la stabilité du rendement grain pour identifier les génotypes stables et performants.

3.2. Analyse de la stabilité du rendement grain

21L'indice P_i. Les valeurs de P_i varient de 1,19, valeur mesurée chez Cyprus₁ à 8,00 pour Semito (Tableau 2). Cet indice mesure la distance qui sépare la performance du génotype d'intérêt de la meilleure performance réalisée au cours de l'année considérée. Rose et al. (2008) mentionnent que les faibles valeurs de P_i sont les plus désirables en sélection parce qu'elles sont la caractéristique des génotypes performants et stables. La corrélation entre les valeurs P_i et les rendements de l'année favorable (r = -0.672, P < 0,01) indique qu'il est possible de sélectionner des génotypes performants et stables parmi les variétés testées. Ces résultats rejoignent ceux de Clarke et al. (1992) qui rapportent une corrélation de -0.91** entre les valeurs de P_i et le rendement du milieu favorable.

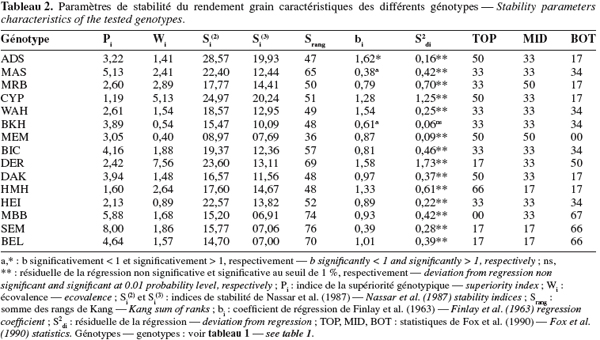
22Les génotypes Cyprus₁ et Heider/Martes//Huevos de Oro sont classés comme étant performants et stables. À l'inverse, MBB et Semito sont instables et peu performants (Tableaux 1 et 2). La sélection des faibles valeurs de P_i identifie donc des génotypes performants et stables. De tels génotypes valorisent nettement mieux les années favorables et se comportent autant, sinon mieux, que les génotypes instables au cours des années contraignantes (Figure 2). La stabilité mesurée par l'indice P_i est de type agronomique. Lin et al. (1988a) mentionnent que ce type de stabilité, à l'inverse de la stabilité de type biologique, intègre la réponse génotypique à la fertilité du milieu. En effet, selon Becker et al. (1988), la stabilité phénotypique peut être de nature statique ou dynamique. La stabilité statique ou biologique indique que le génotype considéré maintient ses performances indépendamment de la variation des conditions du milieu. Un génotype a une stabilité dynamique ou agronomique lorsque ses performances varient en fonction des conditions du milieu. La notion de stabilité a été aussi subdivisée par Lin et al. (1986 ; 1988b) en quatre variantes notées stabilité de type I, II, III et IV. Le type I correspond à la stabilité statique définie par Becker et al. (1988). Le type II correspond à l'écovalence qui mesure la contribution du génotype à l'interaction. La stabilité de type III mesure l'adaptation et un génotype stable dans ce sens présente une meilleure qualité d'ajustement par rapport à la régression sur l'indice de milieu. Le type IV se rapporte à la variation des performances du génotype entre années. Il mesure la capacité du génotype à résister à la variation causée par l'effet année.

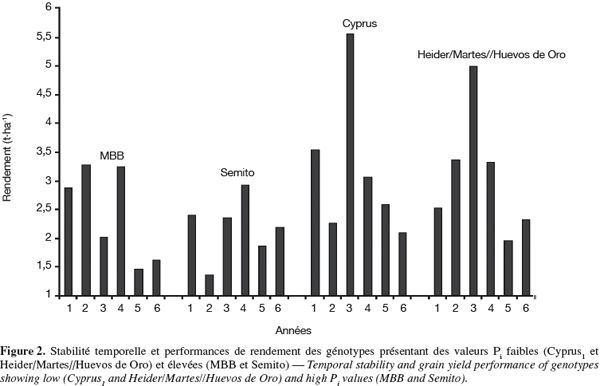
23L'écovalence W_i. L'écovalence (W_i) est une mesure de la contribution du génotype à l'interaction génotype x année. Une valeur W_i nulle ou proche de zéro est indicatrice de la stabilité. Les valeurs W_i élevées sont indicatrices de l'instabilité. Les génotypes Mrb₁₆/Ente//Mario, Belikh₂ et Heider ont de faibles valeurs W_i, ils sont donc stables. Par contre, des valeurs élevées de W_i sont notées chez Cyprus₁ et Deraa qui sont, de ce fait, instables (Tableau 2). La corrélation entre les valeurs W_i et le rendement de l'année favorable est positive (r = 0,691, P < 0,01) suggérant que les génotypes performants sont relativement instables. L'utilisation de ce paramètre de stabilité, en sélection, nécessite de déterminer le poids à donner à la stabilité, relativement au potentiel de rendement, sous conditions semi-arides vu que les agriculteurs recherchent des variétés dont les performances sont stables face à la variabilité interannuelle du climat. Le sacrifice partiel de la stabilité au profit du potentiel de rendement sélectionne des génotypes qui contribuent moyennement à l'interaction. Ceci est le cas du génotype Waha (W_i = 1,54) comparativement aux génotypes jugés instables comme Cyprus₁ (W_i = 5,13) et Deraa (W_i = 7,56) et les génotypes jugés stables comme Belikh₂ (W_i = 0,54) et Mrb₁₆/Ente//Mario (W_i = 0,40) (Figure 3).

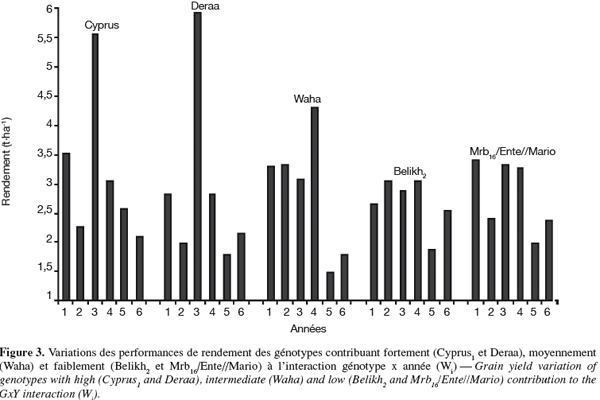
24La régression conjointe. La régression conjointe indique que Adamillo/Duilio//Semito a un coefficient de régression significativement supérieur à l'unité (b > 1). Par contre, Massara₁ et Belikh₂ ont un coefficient de régression qui est inférieur à l'unité (b < 1). Le reste des génotypes évalués ont un coefficient de régression qui ne dévie pas significativement de l'unité (b = 1). Adamillo/Duilio//Semito est donc adapté spécifiquement aux années favorables. Par contre, Massara₁ et Belikh₂ sont spécifiquement adaptés aux années contraignantes. Les autres génotypes montrent une adaptation générale à l'ensemble des années. Parmi ces derniers, Cyprus₁ et Heider/Martes//Huevos de Oro sont les plus performants, en moyenne, sur l'ensemble des années (Tableau 2). Le comportement prédictif de ces génotypes au cours des années dont le potentiel varie de 0,5 à 5 t^.ha^-1, est indiqué en figure 4. Massara₁ se montre performant lors des années dont le potentiel est inférieur à 2 t^.ha^-1. Pour des années dont le potentiel est intermédiaire, entre 2 et 4 t^.ha^-1, Cyprus₁ montre une meilleure adaptation. Au-delà des 4 t^.ha^-1, c'est la zone d'adaptation spécifique de Adamillio/Duilio//Semito (Figure 4).

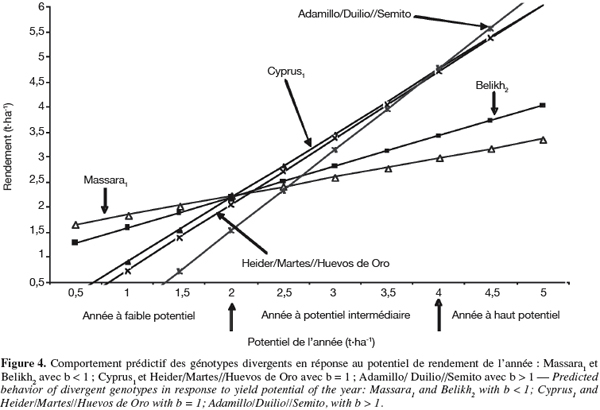
25La résiduelle de la régression (S²_di) est significative pour l'ensemble des génotypes, sauf pour Belikh₂, dont les performances ne dévient pas significativement, de part et d'autre, de la droite de régression. Ce génotype est stable, alors que les autres génotypes sont instables (Tableau 2). Belikh₂ est peu performant comparativement à Cyprus₁ et Deraa qui sont les plus instables (Tableau 1). Du point de vue sélection, l'emploi de S²_di est similaire à celui de W_i. Ces variances mesurent la stabilité de type biologique. Selon Sabaghnia et al. (2006), le génotype idéal est celui dont le rendement grain est le plus élevé, associé à un coefficient de régression qui ne dévie pas significativement de l'unité et des valeurs de W_i et S²_di nulles ou proches de zéro. Parmi les génotypes évalués dans la présente étude, seul Mrb₁₆/Ente//Mario se rapproche de cette définition (Tableau 2).

26Les indices de classement des performances de rendement grain. S_i⁽²⁾ représente la variance des classements du rendement génotypique. Les génotypes stables, d'après ce paramètre, sont ceux qui maintiennent un classement constant au cours des différentes années (Becker et al., 1988). Ils ont donc une faible variance de classement, mais pas forcement un bon classement. S_i⁽²⁾ classe Adamillo/Duilio//Semito et Cyprus₁ comme génotypes instables et Mrb₁₆/Ente/Mario comme génotype stable (Tableau 2). L'indice S_i⁽³⁾ qui représente la somme des carrés des écarts des classements, relativisée par rapport à la moyenne des classements de l'ensemble des années, classe Adamillo/Duilio//Semito et Cyprus₁ comme instables. Par contre, il classe comme stables MBB, Semito, Beliouni et Mrb₁₆/Ente//Mario (Tableau 2). S_i⁽²⁾ et S_i⁽³⁾ sont positivement corrélés entre eux (r = 0,831, P < 0,01) et non corrélés au rendement de l'année favorable ni à celui de l'année contraignante. La sélection de faibles valeurs de ces indices identifie des génotypes aux faibles performances, aussi bien en année favorable qu'en année contraignante. Ceci est le cas de MBB, Semito et Belliouni (Tableaux 1 et 2).

27L'indice S_rang sépare nettement les groupes identifiés par les indices S_i⁽²⁾ et S_i⁽³⁾. Il positionne Mrb₁₆/Ente/Mario dans la classe stable et classe MBB, Semito et Beliouni comme instables (Tableau 2). Les statistiques non paramétriques de Fox et al. (1990) classent Heider/Martes//Huevos de Oro parmi les TOP dans 67 % des années testées. Ce génotype est suivi par Adamillo/Duilio//Semito, Cyprus₁, Mrb₁₆/Ente//Mario et Daki, qui se classent parmi les TOP dans 50 % des années (Tableau 2). Heider/Martes//Huevos de Oro exprime donc une plus grande stabilité et adaptation à la variation des années, alors que Mrb₁₆/Ente//Mario ne présente pas de rendement dans la fraction BOT (Tableau 2). MBB, Semito et Beliouni se classent souvent (67 %) dans la fraction BOT, suite à leur faible potentiel de rendement grain (Tableau 2).

3.3. Similitude des indices

28Chaque indice classe spécifiquement les génotypes évalués (Tableau 3). On note cependant des tendances de similitude entre certaines méthodes comparativement à d'autres. L'analyse des coefficients de corrélation de rang de Spearman indique que P_i est négativement lié aux valeurs S_i⁽³⁾ et TOP ainsi qu'aux rendements de l'année favorable et à la moyenne des rendements de l'ensemble des années (Tableau 4). Les génotypes stables selon l'indice P_i présentent des valeurs de classement élevées pour les indices S_i⁽³⁾ et TOP. W_i est positivement liée à S²_di. S_rang est positivement liée avec BOT et négativement avec TOP (Tableau 4). Les génotypes qui tiennent la tête de classe selon l'indice S_rang (faibles valeurs de S_rang) se classent moins dans BOT (faibles valeurs de BOT) et plus dans TOP (valeurs TOP élevées). Les indices S_i⁽²⁾, S_i⁽³⁾, b et TOP sont positivement corrélés avec le classement des rendements de l'année favorable et avec les moyennes des rendements des six années (Tableau 4).

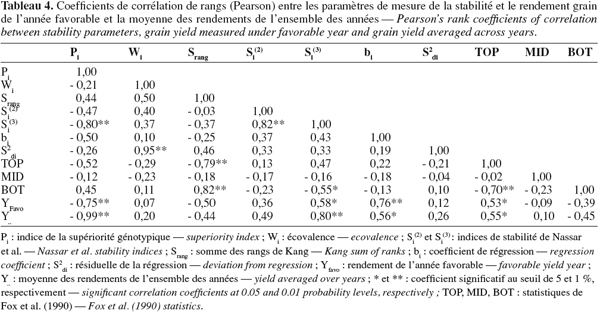
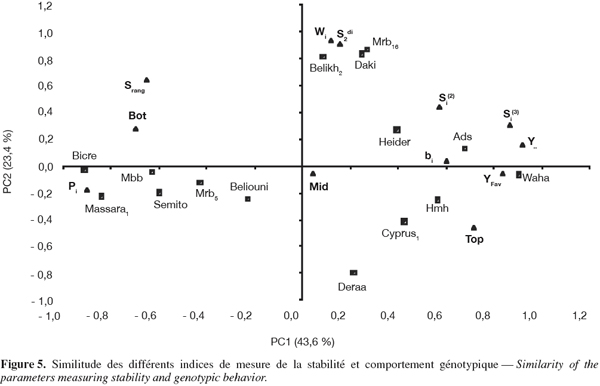
29Pour mieux étudier les relations existantes entre les différents indices, une analyse en composantes principales a été réalisée à partir de la matrice des classements des génotypes sur la base des valeurs prises par les indices de stabilité (Figure 5). Les deux premières composantes principales expliquent 67,0 % (43,6 et 23,4 % pour les facteurs 1 et 2) de la variation totale. Le plan des axes 1 (PC1) et 2 (PC2) de l'analyse en composantes principales groupe les indices selon le type de stabilité. La stabilité agronomique est représentée par l'axe 1 (PC1), alors que la stabilité biologique est représentée par l'axe 2 (PC2) (Figure 5). Le long de l'axe 1 (PC1) s'oppose le classement fait sur la base des indices P_i, BOT et S_rang aux classements basés sur les indices b_i, S_i⁽²⁾, S_i⁽³⁾, TOP. Ces derniers indices ainsi que le rendement de l'année favorable et la moyenne des rendements des six années (effet moyen génotype) sont positivement liés à l'axe 1 (PC1). Ce résultat indique que la stabilité des performances basée sur les faibles valeurs de classement de P_i et de S_rang est similaire à celle définie sur la base des valeurs élevées de classement des indices b_i, S_i⁽²⁾, S_i⁽³⁾ et TOP (Figure 5). Le long de l'axe 2 (PC2) se regroupent l'écovalence (W_i) et la résiduelle de la régression (S²_di) qui sont des indices de stabilité biologique. Leur similitude de classement des génotypes suggère que l'un peut être substitué à l'autre (Figure 5).

4. Discussion

30En sélection, comme en production, le génotype performant est désirable, il l'est encore mieux si ses performances sont stables. Cette stabilité est importante notamment lorsque le milieu (dans le sens année, site, conduite) est sujet à des variations qui causent un changement de l'ordre de classement des génotypes. Les indicateurs des performances et de la stabilité des performances sont utiles en présence d'interaction génotype x année. Les résultats de la présente étude indiquent la présence de l'interaction génotype x année. Ils montrent aussi que les paramètres de stabilité, pris séparément, classent différemment les génotypes évalués. L'analyse en composantes principales groupe les différents indices en deux ensembles, représentant la stabilité agronomique et la stabilité biologique. La stabilité agronomique est mesurée par les indices P_i, b_i, S_i⁽²⁾, S_i⁽³⁾, S_rang et les statistiques de Fox et al. (1990), alors que la stabilité biologique est mesurée par les indices W_i et S²_di.

31La stabilité biologique n'est pas toujours désirable en sélection, lorsque l'objectif est d'augmenter le potentiel de rendement (Kang, 1993). La stabilité agronomique est privilégiée dans ce cas (Becker et al., 1988). Les indices de la stabilité agronomique sont liés à l'effet moyen génotype et au rendement de l'année favorable. Ces résultats corroborent ceux de Sabaghnia et al. (2006) en ce qui concerne le groupage des indices de stabilité. Ils corroborent aussi ceux de Flores et al. (1998) qui mentionnent que l'indice TOP est associé positivement à la moyenne des rendements calculée sur l'ensemble des milieux. Kang et al. (1991) mentionnent que l'indice S_rang est lié avec les performances de rendement et de ce fait, il représente la stabilité agronomique. Nassar et al. (1987) mentionnent que S_i⁽²⁾ et S_i⁽³⁾ sont liés entre eux et représentent la stabilité agronomique, ce qui rejoint les résultats de la présente étude. Pour une application en sélection dans une région semi-aride, les résultats suggèrent d'utiliser l'indice P_i lorsque la sélection est orientée vers la recherche de la performance et de la stabilité. L'indice W_i est à utiliser lorsque c'est la stabilité qui est privilégiée. Une alternative aussi intéressante est l'utilisation de l'indice de Fox et al. (1990) qui donne la proportion de classement dans le tiers supérieur des rendements. Les indices P_i et TOP identifient Cyprus₁ et Heider/Martes//Huevos de Oro comme les plus stables et performants dans le cadre de cette étude.

5. Conclusion

32En présence d'interaction génotype x environnement, l'analyse de la stabilité des performances, au même titre que la performance, est très importante. Plusieurs méthodes sont décrites dans la littérature. L'étude comparative de ces méthodes groupe les indices de la stabilité en deux ensembles, l'un représentant la stabilité agronomique et l'autre la stabilité biologique. Parmi les paramètres de stabilité étudiés, les indices P_i et TOP identifient des génotypes performants et stables. Dans le cas où la stabilité prime au détriment de la performance, l'écovalence est plus utile comme indice de stabilité. W_i identifie Belikh₂ et Mrb₁₆/Ente//Mario comme génotypes stables. Les résultats de cette étude souffrent cependant du fait que la notion de milieu est prise dans le sens seulement d'année, alors que l'effet année est partiellement imprévisible. De plus, le nombre d'années étudiées est très limité, ce qui affecte la précision du calcul des indices. L'étude gagnerait à être répétée sur plusieurs sites pour valider ces résultats qui, néanmoins, corroborent et rejoignent les résultats d'études citées en référence.

Bibliographie

Pour citer cet article

A propos de : Amar Benmahammed

A propos de : Hind Nouar

A propos de : Leila Haddad

A propos de : Zahra Laala

A propos de : Oulmi Abdelmalek

A propos de : Hamenna Bouzerzour