- Accueil
- volume 18 (2015)
- number 1
- What does the interface on the fresh-saltwater distribution map of the Belgian coastal plain represent?
Visualisation(s): 2201 (24 ULiège)
Téléchargement(s): 282 (4 ULiège)
What does the interface on the fresh-saltwater distribution map of the Belgian coastal plain represent?

Document(s) associé(s)
Annexes
Abstract
Knowing the distribution between fresh and saline groundwater is imperative for a sustainable and integrated management of water resources in coastal areas. The Belgian coastal plain forms no exception. Based on vertical electrical soundings (VES) and available geological data maps were published in 1974 and 1989 that show the depth to the interface between the freshwater and the underlying saltwater. This interface was defined as the 1.5 g/L total dissolved solids surface and interface depth was depicted using classes based on depth intervals. Recent developments in geophysical prospection make it possible to collect data with a high spatial resolution. The comparison with 1974 and 1989 maps is thereby not so straightforward as it seems. Therefore, this paper elucidates the nature of the mapped interface and its relation with salinity. The interface, as determined by VES, is the boundary between a freshwater and saltwater electrical distinct layer. The resistivity of this interface can vary between 1 and 75 Ω∙m. However, this translates in a narrow range of salinities for which 1.5 g/L represents a mean. Comparing new data with the old maps thus takes more than simply comparing the depth to a certain resistivity value.
Table des matières
1. Introduction
1The 1974 and 1989 maps that show the depth to the freshwater-saltwater interface (De Breuck et al., 1974, 1989), commonly known as the salinization maps, visualize the complex distribution between freshwater and saltwater in the coastal area. This distribution is the result of the geologic evolution after the last ice age and recent human intervention because of land reclamation and impoldering (e.g. Vandenbohede & Lebbe, 2012; Vandenbohede, 2014). The maps remain an important instrument for research, form a source of data for applied studies and form the base of government groundwater policy.
2The maps are mainly based on surface geophysical methods: the 1974 map for instance is based upon more than 1700 resistivity soundings. More data were obtained after the publication of the original maps. Vandenbohede et al. (2010) compared recent data sets with the 1974 map of the central coastal plain and concluded that the maps stood the test of time: the overall salinity pattern in the coastal plain is very well represented and new data only fill in local details.
3However, new methods such as electrical resistivity tomography (Goldman & Kafri, 2006), cone penetration tests (Dietrich & Leven, 2006), or airborne electromagnetic surveys (Siemon et al., 2009) provide the opportunity to collect data about the subsoil, including the salinity distribution, with a high spatial resolution not available at the time of construction of the maps. The authors recently received a number of questions how such high resolution geophysical data could be compared with and could complement the existing maps. Hence a better definition of the exact nature of the mapped interface, indicated on the maps as the 1.5 g/L total dissolved solids (TDS) surface, is required.
4Therefore, we elucidate in this paper the background, the geophysical data interpretation and the construction of the salinization maps. Firstly we review briefly the genesis of the maps and the surface geophysical method that was used in terms of freshwater – saltwater interface derivation. Secondly, the nature of the mapped interface and its relation with a TDS value are discussed and illustrated with an example.
2. Mapping the interface
2.1. Background of the maps
5A surface geophysical method, the DC resistivity electrical method, was used to map the freshwater-saltwater distribution in the Belgian coastal plain. The decrease in bulk resistivity with pore water resistivity is used to locate brackish or saline groundwater. The method’s main advantages are the relatively low instrument cost and simplicity of operation. DC resistivity was the first surface geophysical method used for water quality determination, applied in island and coastal environments in the late 1930s (Swartz, 1937, 1939).
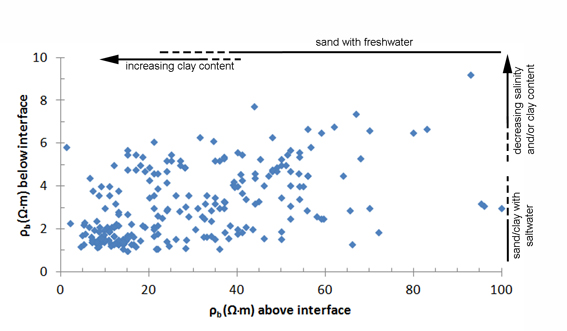
6Scientific interest in the distribution between freshwater and saltwater in the Belgian coastal plain dates from the beginning of the 20th century (d’Andrimont, 1902, 1904). A first attempt to map the distribution, i.e. the interface between freshwater and saltwater, was made during the summer of 1942 and the spring of 1943. The area west of the Yser river was investigated by a geophysical survey (DC resistivity) of the Erdelektrischer Messtrupp 5 of the German army. This was part of a larger mapping survey covering the area between Calais (France) and Nieuwpoort (Thiele, 1943; 1952) (Fig. 1A). Between measurement locations, interface depth was interpolated without considering the underlying geology which gave a rather artificial end-result. De Paepe & De Breuck (1958) used the data set of Thiele to create a more logical map (Fig. 1B) taking into account the Quaternary geology that became available in the 1950s as a result of the soil mapping. Experience with a geo-electrical survey of the province of West-Vlaanderen (De Moor & De Breuck, 1964) further illustrated the possibility to map the interface depth in an area with a complex salinity distribution. Because of the socio-economic importance of freshwater (e.g. De Paepe & De Breuck, 1958), new field work was initiated in the late 1960s and early 1970s to map the interface (Fig. 1C). This was done in the framework of a number of MSc dissertations for the western coastal plain (Burvenich, 1970; Tjoa, 1971; Joye 1970; Maes, 1970) and surveys of the eastern coastal plain. The results were combined in the well-known 1974 map (Fig. 1D). It shows the depth to the interface represented by means of classes (<2 m, 2-5 m, 5-10 m, etc.) for the complete Belgian coastal plain. This work was continued in the province of Zeeland (The Netherlands) which resulted in the 1989 map.
7Of notice is the increase in detail between the 1943 and 1974 map. This is not only an evolution because of the compilation of new salinity data. Geological data from drillings and the soil mapping, and understanding of the processes to explain the salinity distribution (De Breuck & De Moor, 1975) were incorporated in the later maps.
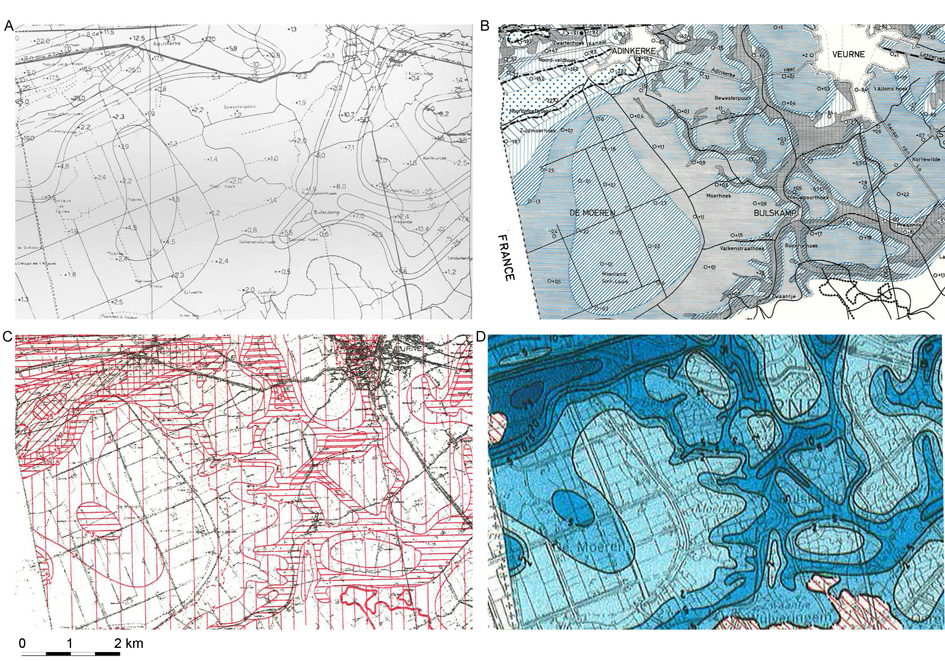
8Figure 1. Different stages in the making of the salinization map of the Belgian coastal plain illustrated for the area between Veurne and the Belgian-French border: (A) first attempt by Thiele (1943),(B) reinterpretation by De Paepe and De Breuck (1958), (C) new field surveys (Burvenich, 1970), and (D) the 1974 map by De Breuck et al. (1974). North is up.
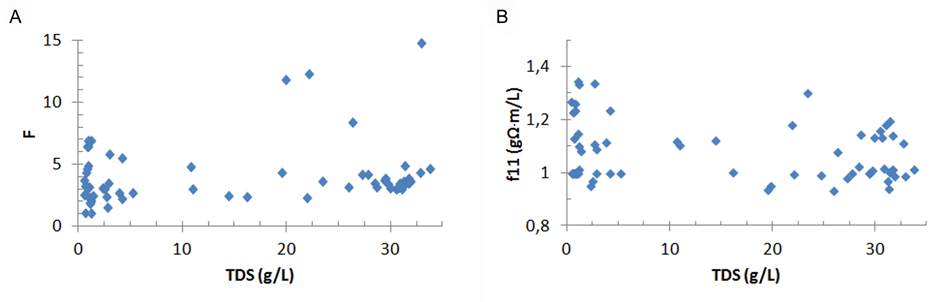
2.2. From measurement to interface depth
9The DC method introduces an electrical current into the ground through current electrodes and measures the resulting electrical potential difference between two potential electrodes. The combination of Ohm's and Pouillet's laws relates resistivity ρ (Ω∙m) with the current I (A) and the voltage difference ΔV (V) between the measuring electrodes:
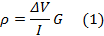
10G (m) is a geometric factor that varies with electrode configuration and spacing.
11In most cases, a four-electrode array is applied such as the Werner or Schlumberger arrangement. The distance between electrodes is varied to measure the vertical variation in resistivity, a technique which is known as vertical electrical sounding or VES. The depth of investigation depends on the distance between the current electrodes. For an electrical homogeneous isotropic subsurface, the measured resistivity directly gives the bulk (i.e. matrix and pore water) resistivity ρb of the subsoil. Otherwise, the measured resistivity is a combination of the bulk resistivity of the different electrical distinct layers, called an apparent resistivity. The aim of the interpretation of a VES is to derive the bulk resistivity ρb and thickness of the different electrical distinct layers. Freshwater and saltwater are considered to provide such an electrical distinct layer. The derivation of the bulk resistivity is an inverse problem, the solution of which is non-unique. Particularly, in 1D VES inversion the principles of equivalence and suppression limit the interpretation of the results in addition with possible 2D effects.
2.3. From bulk resistivity to TDS
12Bulk resistivity is related to pore water resistivity ρw through the formation factor F (-), known as Archie’s law (1942):
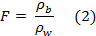
13Archie's law postulates that the rock matrix is non-conductive, which is only appropriate in the case of sand. Otherwise, an additional term is needed to include the resistivity ρm (Ω∙m) of the sediment/rock matrix (Patnode & Willie, 1950):
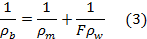
14TDS can be related to pore water conductivity using the UNESCO 1980 equation of state (Fofonoff & Millard, 1983). In most cases however, a simple linear relation between TDS and pore water conductivity through a factor f11 (gΩ∙m/L) can be used. The relation between pore water resistivity and TDS (g/L) is then:
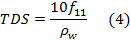
15The subscript 11 points to the fact that resistivity at 11°C is used since this is the mean temperature value for (shallow) groundwater in Belgium. Lebbe & Pede (1986) suggest a mean value of 4 for F and 1 gΩ∙m/L for f11.
2.4. Identifying saltwater
16It is difficult to assign a low resistivity value either to the presence of clay, salt water or a combination of both. Prior information, such as for instance the presence of clay, helps in the interpretation. Based on geophysical surveys in West-Vlaanderen (De Moor & De Breuck, 1964), in the Flemish Valley and eastern coastal plain (Maréchal et al., 1957) and summarized by Maréchal et al. (1970), typical ranges of the bulk resistivity for different materials were formulated (Table 1) and used for the interpretation of the VES measurements. Of notice is the relatively large range for sediments with saline pore water. However, a bulk resistivity smaller than 6 Ω∙m was considered as a value for clearly salinized sediments and a value of 3 Ω∙m for highly salinized sediments.
17The 3 Ω∙m translates in today terms of saline pore water, i.e. more than 10 g/L TDS, in case of sandy sediments. For sands, values between 6 and 10 Ω∙m still represent an increased salinity, up to 5 g/L. The bulk resistivity changes importantly with both TDS and sediment matrix resistivity if the latter parameter becomes smaller than 10 Ω∙m (equation 3). In such case (i.e. clay or sediments with an important clay content), a bulk resistivity lower than 10 Ω∙m can be attributed to either a high TDS or a high clay content, or the combination of both. However, when the salinity increases the relative importance of the pore water conductivity increases and the bulk resistivity is related directly to the pore water resistivity and thus TDS. Consequently, a bulk resistivity lower than 3 Ω∙m can in most cases be attributed to saline pore water.
|
natural material |
bulk resistivity ρb (Ω∙m) |
|
dry sand |
100 - 1000 |
|
sand with fresh pore water |
40 - 100 |
|
loam with fresh pore water |
25 - 40 |
|
arenaceous clay with fresh pore water |
15 - 30 |
|
clay with fresh pore water |
6 – 15 |
|
sediments with saline pore water |
1 - 10 |
18Table 1. The range of bulk resistivity for different natural materials (after De Moor and De Breuck, 1964, Maréchal et al., 1957 and Maréchal et al., 1970).
3. What does the 1974 and 1989 interface represent?
3.1. Freshwater and saltwater electrical distinct layers
19Evidently, there is a fundamental difference between mapping geological layers or salinity with VES: geological layers provide in most cases sharp boundaries whereas this is generally not the case for salinity profiles. The transition zone between the freshwater and underlying saltwater is thereby seldom resolved beyond an interface (i.e. a specific value for the bulk resistivity) and this interface lies within the occurring transition zone. Before focusing on the nature of this interface, we describe the electrical distinct layers which were interpreted as the freshwater and saltwater layers.
20VES measurements were fitted to pre-calculated theoretical curves by a curve-matching procedure (e.g. Thiele, 1952; Zohdy et al., 1974). In most cases, a two- or three-layer electrical model of the subsoil was used. A two-layer model distinguishes between freshwater and saltwater or between freshwater and an underlying clay layer. A three-layer model distinguishes between the unsaturated zone, fresh water and salt water, or between fresh water, salt water and an underlying clay layer. In all cases a depth to an interface, i.e. the depth to the boundary between the electrical distinct layers representing the freshwater and saltwater, was derived. The calculated bulk resistivity of the layers above and below this interface shows a wide range of values (Fig. 2).
21Bulk resistivity of the freshwater electrical layer varies between 5 and 100 Ω∙m. This corresponds with a clay or sand matrix filled with fresh pore water. An increasing clay content results in a lower value of the bulk resistivity. Bulk resistivity of the saltwater electrical layer varies between 0.5 and 9 Ω∙m. In most cases, the bulk resistivity is below the value of 6 Ω∙m that was indicated before as an upper limit for clearly salinized sediments. Bulk resistivity of the freshwater and saltwater electrical layers indicates that an interface between the freshwater and the underlying saltwater was determined in sediments showing a wide range of bulk resistivities, i.e. representing different sand, silt or clay contents. In a number of cases, the complete Quaternary aquifer is fresh. This is possible in the dunes or in case of thick freshwater lenses in the polders.
22Figure 2. Plot of the bulk resistivity below the interface mapped by De Breuck et al. (1974) as a function of the bulk resistivity above the interface. This is based on the work of Burvenich (1970), Tjoa (1971), Joye (1970), and Maes (1970).
3.2. TDS of the interface?
23The formation factor F and conversion factor f11 are two important factors to recalculate TDS from the bulk resistivity. Figure 3 shows these factors as a function of TDS for sediments in the eastern Belgian coastal plain, as sampled by Clays (1999), Hermans (1999) and Van Haecke (1998). Bulk resistivity is measured with geophysical borehole loggings, pore water resistivity is measured using water samples and TDS is calculated from chemical analyses of water samples. This is shown for sand sediments and Archie’s law (eq. 2) is used as simplification to relate TDS, pore water resistivity and bulk resistivity. With this assumption, the formation factor F varies between 1 and 15 with a mean value of 4.4. The conversion factor f11 varies between 0.9 and 1.4 with a mean value of 1.07.
24Figure 3. Formation factor F and conversion factor f11 as a function of TDS, derived for sandy sediments in the eastern Belgian coastal plain.
25In general, a VES derived interface between the freshwater and saltwater electrical layer is in the middle of the transition zone (Stewart, 1990). However, the non-linearity of equation 4, whereby the pore water conductivity changes linearly with TDS but is the reciprocal of resistivity, gives rise to a different transition zone in terms of pore water or bulk resistivity than in terms of TDS. In a hypothetical example (Fig. 4), TDS as a function of depth is considered using a sigmoid function and the transition zone can be characterised by the spatial moment method (de Louw et al., 2011, Eeman et al., 2011). The pore water resistivity change with depth is described by a normal distribution function, from which the centre of mass (first moment) indicates the centre of the transition zone and the variance (second moment) is a measure of the extent of the transition zone. The transition zone is 15 m wide with its centre at 20 m depth in the example. TDS changes from 0.5 to 30 g/L. The pore water resistivity (calculated with f11 = 1) changes quickly in the upper part of the TDS transition zone, but becomes almost constant in the lower part. Consequently, there is an upward shift of the transition zone in terms of resistivity compared with the transition zone in terms of TDS. For this example, the centre of the transition zone in terms of pore water resistivity is found at a depth of 15.9 m.
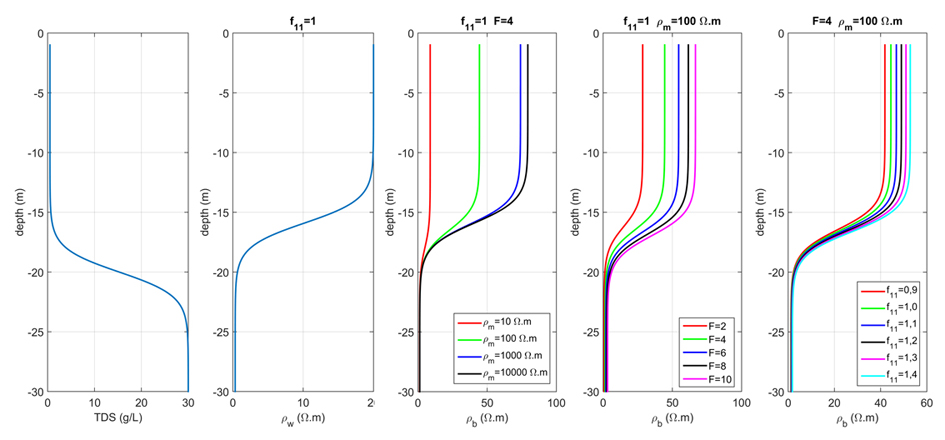
26Figure 4. Hypothetical salinity profile and the resulting pore water and bulk resistivity as a function of depth for a range of values of F, ρm and f11.
27With the hypothetical TDS profile, the bulk resistivity is calculated for a number of parameter combinations of the matrix resistivity ρm, the formation factor F, and the f11 (Fig. 4), the latter values varying according to observed ranges (Fig. 3). Evidently, the transition zone in the bulk resistivity is shifted upward with regard to the TDS profile. This upward shift increases with increasing matrix resistivity ρm, decreasing formation factor F, and increasing f11 although the effect of the latter parameter being very small. The transition zone in terms of bulk resistivity is found at a depth ranging from 17.9 to 15.9 m with a mean value of 16.5 m in this example. This corresponds with a TDS ranging between 1 and 3.5 g/L with a mean value of 1.4 g/L. The TDS above and under the interface also influences this result. An increase in salinity above the interface will increase the salinity of the centre of the transition zone in terms of resistivity. In the Belgian coastal plain TDS of fresh water varies between 0.5 and 1 g/L (Vandenbohede & Lebbe, 2012) but also higher values can be found above the transition zone depending on local circumstances.
28These calculations are repeated for a wide range of parameter combinations to obtain a general picture. The formation factor varies between 1 and 10 with a step of 0.25 and the factor f11 varies between 0.9 and 1.4 with a step of 0.025. Matrix resistivity varies between 1 and 1000 Ω∙m. To equally weigh the contribution of clay and sand matrices, the interval between 1 and 100 Ω∙m is subdivided into 250 intervals whereas the interval between 100 and 1000 Ω∙m is equally subdivided into 250 intervals. Salinity values of 0.5, 0.75 and 1 g/L above the interface are considered. For each of these 388,500 combinations, the centre of the transition zone in terms of bulk resistivity (i.e. the interface derived from VES) is determined and the corresponding TDS is calculated. The interface depth in terms of bulk resistivity varies thereby between 18.8 and 20 m.
2972 % of the combinations result in a TDS at the centre of the transition zone in terms of resistivity which lies between 1 and 2 g/L if the TDS of the fresh water is 0.5 g/L (Fig. 5A). This decreases to 66 % and 37 % if the TDS of the freshwater is 0.75 and 1 g/L respectively. The TDS of the salt water has a similar effect: 67 % of the combinations result in a TDS at the centre of the transition zone in terms of resistivity that is between 1 and 2 g/L if the TDS of the salt water is 15 g/L (not shown). However, the percentage does not change importantly if salt water TDS is above 20 g/L due to the fact that pore water salinity becomes more important than sediment matrix resistivity to determine the bulk resistivity. High TDS values (up to 10 g/L) correspond with lower values for the bulk resistivity (Fig. 5B). In these cases, the range for bulk resistivity at the centre of the interface is limited. In sand sediments a wider range for the bulk resistivity at the centre of the interface is possible, being function of the formation factor, factor f11 and the matrix resistivity. Changing the width of the transition zone only has a minor influence on these calculations.
30The hypothetical example (Fig. 4) illustrates the wide range of bulk resistivity values which can occur above the transition zone and the more limited range of values below it. As a consequence the bulk resistivity at the centre of the transition (Fig. 5B) also shows a wide range of values. This is exactly what is also concluded from the field measurements (Fig. 2). However this compares with a more limited range of pore water TDS values for the centre of the transition zone in terms of bulk resistivity for which a value between 1 and 2 g/L is found in many cases (Fig. 5A).
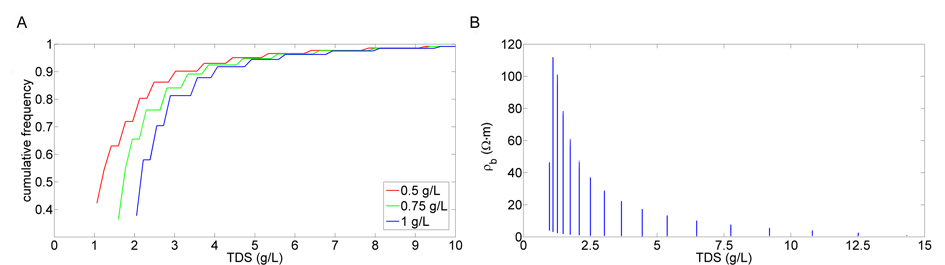
31Figure 5. Cumulative frequency of the TDS at the centre of the transition zone for different TDS values of the freshwater (A) and TDS versus the bulk resistivity at the centre of the transition zone for a freshwater TDS of 0.5 g/L (B).
4. Field example
32There are only a few field examples where VES measurements can be compared with subsurface measurements in boreholes and drilling descriptions. De Breuck (1975) provides data for such a case in the coastal plain.
33The example is located near Blankenberge. The upper 10 m of the vertical profile consists of clayey and silty sand with intercalations of peat. The lower part of the profile consists of sand. The Tertiary substratum occurs at a depth of 27.5 m. Figure 6 shows the apparent resistivity versus the electrode distance as measured by the VES and the resulting electrical model. Exceptionally, the VES is interpreted with a four layer electrical model. The first layer has a thickness of 1.4 m, bulk resistivity of 13.5 Ω∙m, and corresponds with the unsaturated zone. The second zone has a thickness of 7.6 m, a bulk resistivity of 5 Ω∙m, and represents the clayey and silty sand upper part of the profile. The third layer has a thickness of 8 m and a relatively high bulk resistivity of 45 Ω∙m. The fourth layer has a low bulk resistivity (1.6 Ω∙m). The first three layers represent differences between unsaturated and saturated zone and lithological variations. The difference between the third and fourth layer cannot be attributed to geology but is due to saline pore water in the latter layer. Consequently, the interface is located at a depth of 17 m.
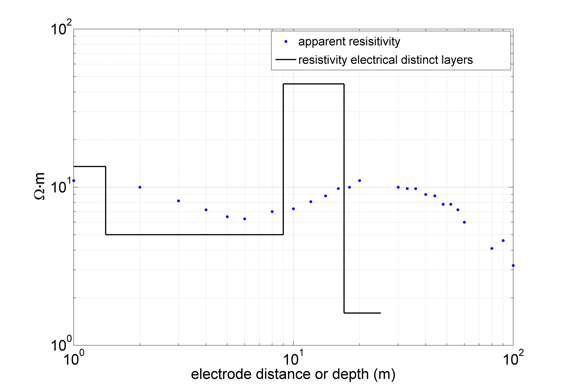
34Figure 6. The apparent resistivity versus the electrode distance compared with the resistivity as function of depth in the applied electrical model in case of the field example.
35The resistivity of the pore water was measured by a fluid-resistivity log in a fully screened borehole and shows an s-shaped transition zone (Fig. 7), comparable with the hypothetical example. TDS of the freshwater is 1g/L when using a conversion factor f11 of 1. Depth to the interface by VES (17 m) corresponds with a TDS of 1.8 g/L. A bulk resistivity ranging between 15.4 and 18.2 Ω∙m is computed, based on a matrix resistivity ranging between 50 and 100 Ω∙m.
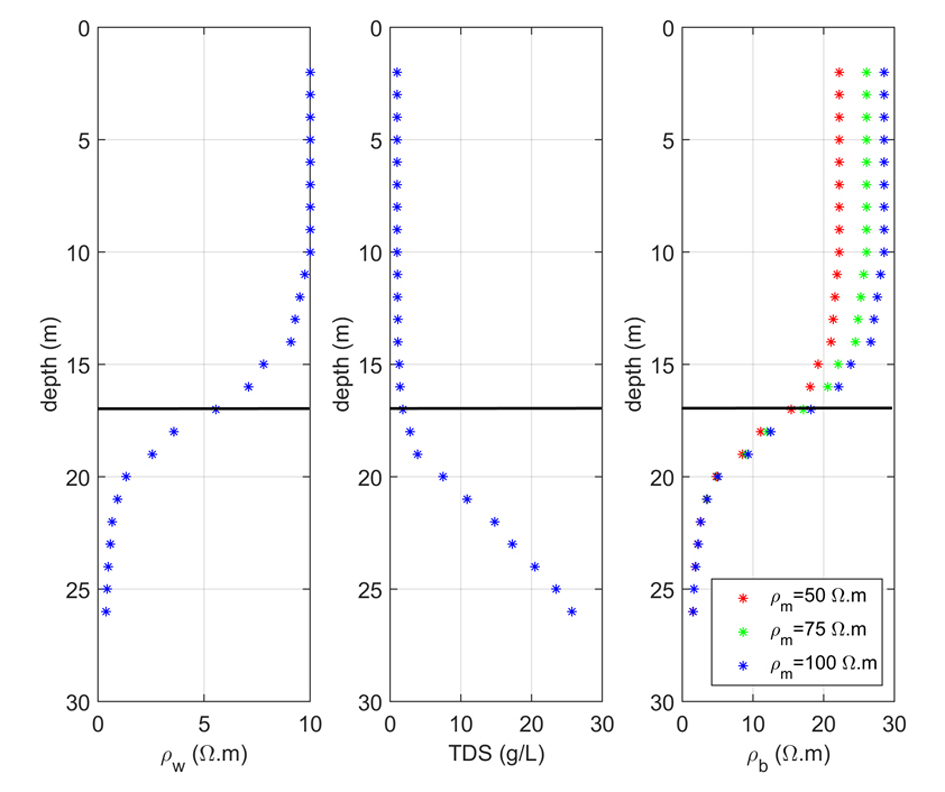
36Figure 7. Measured pore water resistivity and calculated TDS and bulk resistivity as a function of depth for the example. Black lines indicate the location of the interface as determined by VES.
5. Conclusions
37With VES measurements, the transition zone between freshwater and saltwater was characterized by a single interface, i.e. the interface between freshwater and saltwater electrical distinct layers. The depth to this interface was plotted on the 1974 and 1989 salinization maps. A wide range of bulk resistivity values are found for the electrical distinct layers that represent the freshwater zone above the interface and the saltwater zone below the interface. This means that the resistivity at this interface depth in the transition zone is also not a single value but can vary, in most cases between 1 and 75 Ω∙m, depending on the resistivity of the matrix ρm, the formation factor F, the conversion factor f11 and quality of the freshwater and saltwater. However, this translates into a less wide range of TDS values at this interface depth in the transition zone. More than half of them are in the range between 1 and 2 g/L. Larger values are in most cases found in clay rich sediments (low matrix resistivity) or with a relatively high salinity in the freshwater part of the profile (1 g/L or more).
38This means that the interface that is plotted on the 1974 and 1989 maps represents not a single TDS value. However, the value of 1.5 g/L, as is indicated on the maps, forms a representative mean at many (not to say most) locations. Moreover, the uncertainty on the exact TDS value of the interface at a given location was taken care of by mapping the depth to the interface in classes of depth intervals (<2 m, 2-5 m, 5-10 m, etc.) rather than plotting the measured value. The soundness of this method of defining the interface and its depth representation was proven by a recent verification of the map with post-1974 data (Vandenbohede et al., 2010).
39These conclusions have implications for the comparison of the 1974 and 1989 maps with new geophysical survey results. Evidently, it makes no sense to compare the depth of a certain iso-resistivity surface with these maps since in almost any case, apples and oranges are compared. An alternative should be considered by comparing the depth to the centre of the transition zone visible on a measured resistivity profile (i.e. apparent or bulk resistivity as function of depth) with the old interface depth. Differences based on resolution of different geophysical methods are, however, unavoidable. Also, the use of additional information such as borehole measurements or water quality samples in the interpretation of surface geophysical measurements is recommended since it adds the inclusion of actual subsurface bulk resistivity or pore water TDS. (e.g. de Louw et al., 2011; Hermans et al., 2012). Equally, the use of salinity distribution derived through numerical groundwater flow modelling, opens interesting prospects (e.g. Beaujean, 2014; Faneca Sànchez, 2012; Vandenbohede et al., 2011).
40When comparing new data with the 1974 and 1989 maps, it should not be forgotten that the 1974 and 1989 maps are the end results of a long period of data gathering and a number of intermediate stages of mapping. Not only the water quality data (from geophysical surveys or water samples) but also geological data (soil mapping and drillings) were used to interpolate between measurement locations. Understanding of the process of freshening of an initially saline Quaternary aquifer was equally put into the maps. By analogy, the inclusion of lithological information, TDS data and/or borehole logs to solve the electrical inverse problem is therefore recommended when interpreting new data.
41Finally, one should also be very careful to state that differences between current data and the 1974 and 1989 maps are due to evolutions in the salinity distribution. Therefore, one must be sure that similar data (i.e. an equal iso-TDS surface) are compared and that effects of different resolution of geophysical methods and issues of data interpolation between measurement points are ruled out.
6. Acknowledgement
42Alexander Vandenbohede was supported by the Fund for Scientific Research — Flanders (Belgium) as a postdoctoral fellow. Perry de Louw and an anonymous reviewer are acknowledged for their constructive comments.
7. References
43Archie, G.E., 1942. The electrical resistivity log as an aid in determining some reservoir characteristics. Petroleum Transactions of AIME, 146, 54–62.
|
Burvenich, T., 1970. Geo-elektrisch onderzoek op de kaartbladen De Moeren-Veurne. MSc dissertation, Ghent University. |
44Clays, S., 1999. Hydrogeologisch en hydrogeochemisch onderzoek van het westelijk deel van de Uitkerkse polder bij Wenduine. MSc dissertation, Ghent University.
45d'Andrimont, R., 1902. Notes sur l'hydrologie du littoral belge. Annales de la Société géologique de Belgique, 29, M129-M144.
46d’Andrimont, R., 1904. L’allure des nappes aquifères contenues dans de terrains perméables en petit, au voisinage de la mer. Annales de la Société géologique de Belgique, 32, M101-M113.
47Beaujean, J., Nguyen, F., Kemna, A., Antonsson, A. & Engesgaard, P., 2014. Calibration of seawater intrusion models: Inverse parameter estimation using surface electrical resistivity tomography and borehole data. Water Resources Research, 50(8), 6828-6849.
48De Breuck, W., 1975. Hydrogeological SWIM-excursion to the coastal region of Belgium. Proceedings 4th Salt Water Intrusion Meeting, Gent, 202-215.
49De Breuck, W. & De Moor, G., 1975. The evolution of the coastal aquifer of Belgium. Proceedings 4th Salt Water Intrusion Meeting, Gent, 158-172.
50De Breuck, W., De Moor, G., Maréchal, R. & Tavernier, R., 1974. Diepte van het grensvlak tussen zoet en zout water in de freatische laag van het Belgische kustgebied (1963-1973). Verziltingskaart. Brussel, Militair Geografisch Instituut.
51De Breuck, W., Beeuwsaert, E. & Vandenheede, J., 1989. Diepte van het grensvlak tussen zoet en zout water in de freatische watervoerende laag van noordelijk Vlaanderen (1974-1975). Verziltingskaart Zeeuws-Vlaanderen. Universiteit Gent, Laboratorium voor Toegepaste Geologie en Hydrogeologie.
52de Louw, P.G.B,, Eeman, S., Siemon, B., Voortman, B.R., Gunnink, J., van Baaren, E.S. & Oude Essink, G.H.P., 2011. Shallow rainwater lenses in deltaic areas with saline seepage. Hydrology and Earth System Science, 15, 3659-3678.
53De Moor, G. & De Breuck, W., 1964. Geo-elektrisch onderzoek bij de geologische overzichtskartering van West-Vlaanderen. Natuurwetenschappelijk Tijdschrift, 46, 215-240.
54De Paepe, P. & De Breuck, W., 1958. De drinkwatervoorziening van de landbouwbedrijven in West-Vlaanderen. Brugge, Provinciaal Bestuur West-Vlaanderen, Ekonomische Monografieën.
55Dietrich, P. & Leven, C., 2006. Direct push-technologies. In Kirsch, R. (ed.), Groundwater geophysics, a tool for hydrogeology. Springer, Berlin, 321-340.
56Eeman, S., Leijnse, A, Raats, P.A.C. & S.E.A.T.M. van der Zee, 2011. Analysis of the thickness of a freshwater lens and of the transition zone between this lens and upwelling saline water. Advances in Water Resources, 34, 291-302.
57Faneca Sànchez, M., Gunnink, J.L., van Baaren, E.S., Oude Essink, G.H.P, Siemon, B., Auken, E., Elderhorst, W. & de Louw, P.G.B., 2012. Modelling climate change effects on a Dutch coastal groundwater system using airborne electromagnetic measurements. Hydrology and Earth System Sciences, 16(12), 4499-4516.
58Fofonoff, N.P. & Millard Jr, R.C., 1983. Algorithms for the computation of fundamental properties of seawater. UNESCO technical papers in marine sciences, 44, 1-53.
59Goldman, M. & Kafri, U., 2006. Hydrogeophysical applications in coastal aquifers. In: Vereecken, H., Binley, A., Cassiani, G., Revil, A. & Titov, K. (eds), Applied Hydrogeophysics. Nato Science Series, Serie IV, Earth and Environmental Sciences, 71, Springer, Dordrecht, 233–254.
60Hermans, A., 1999. Hydrogeologisch en hydrogeochemisch onderzoek van het duingebied te Wenduine - De Haan. MSc dissertation, Ghent University.
61Hermans, T., Vandenbohede, A., Lebbe, L., Martin, R., Kemna, A., Beaujean, J. & Nguyen, F., 2012. Imaging artificial salt water infiltration using electrical resistivity tomography constrained by geostatistical data. Journal of Hydrology, 438-439, 168-180.
62Joye, M., 1970. Geo-elektrisch onderzoek in de streek van Nieuwpoort-Oostduinkerke. MSc dissertation, Ghent University.
63Lebbe, L. & Pede, K., 1986. Salt-fresh water flow underneath old dunes and low polders influenced by pumpage and drainage in the western Belgian coastal plain. Proceedings 9th Salt Water Intrusion Meeting, Delft, 199-220.
64Maes, M., 1970. Geo-elektrisch onderzoek in de westelijke kustvlakte : kaartbladen Lampernisse en Lo. MSc dissertation, Ghent University.
65Maréchal, R., De Breuck, W. & De Moor, G., 1957. Geo-elektrische prospectie in het Kustgebied en in de Vlaamse Vallei. Half-jaarlijks Tijdschrift Becewa, 14, 1-7.
66Maréchal, R., De Breuck, W., De Moor, G. & Henriet, J.P., 1970. Geo-elektrische prospektie bij het hydrologisch onderzoek. Informatieblad Navewa, 192, 2-13.
67Patnode, H.W. & Willie, M.R.J. 1950. The presence of borehole geophysics to water resources investigations. Techniques of water-resources investigations of the USGS, Book 2, chapter E1.
68Siemon, B., Christiansen, A.V. & Auken, E., 2009. A review of helicopter-borne electromagnetic methods for groundwater exploration. Near Surface Geophysics, 7(5-6), 629-646.
69Stewart, M., 1990. Rapid reconnaissance mapping of fresh-water lenses on small oceanic islands. Geotechnical and Environmental Geophysics, 2, 57-66.
70Swartz, J.H., 1937. Resistivity studies of some salt-water boundaries in the Hawaiian Islands. American Geophysical Union Transactions, vol 18.
71Swartz, J.H., 1939. Part II - Geophysical investigations in the Hawaiian Islands. American Geophysical Union Transactions, vol 20.
72Thiele, H., 1943. Tiefenkarte der Grenze Süsswasser-Salzwasser bezogen auf Normal-Null (französisch und belgisch Flandern), 1/25000, 8 Blätter, Deutsche Heereskarten.
73Thiele, H., 1952. Teil II Die Geoelektrik in der Wassererschliessung. In: Deutschen Verein von Gas- und Wasserfachmännern. Die Wassererschliessung. Vulkan-Verlag, Essen.
74Tjoa, K.H., 1971. Geo-elektrisch onderzoek in de streek van Lombardsijde-Westende. MSc dissertation, Ghent University.
75Vandenbohede, A., Courtens, C., Lebbe, L. & De Breuck, W., 2010. Fresh-salt water distribution in the central Belgian coastal plain: an update. Geologica Belgica, 11(3), 163-172.
76Vandenbohede, A., Hinsby, K., Courtens, C. & Lebbe, L., 2011. Flow and transport model of a polder area in the Belgian coastal plain: example of data integration. Hydrogeology Journal, 19(8), 1599-1615.
77Vandenbohede, A. & Lebbe, L., 2012. Groundwater chemistry patterns in the phreatic aquifer of the central Belgian coastal plain. Applied Geochemistry, 27, 22-36.
78Vandenbohede, A., 2014. Quartair van de Kustvlakte en polders van de Westerschelde. In Dassargues, A. & Walraevens, K. (eds), Watervoerende lagen en grondwater in België / Aquifères et eaux souterraines en Belgique, Gent, Academia Press, 5-15.
79Van Haecke, K., 1998. Hydrogeochemisch onderzoek naar de zoet-zoutwaterverdeling langs een profiel loodrecht op de kustlijn (Wenduine – De Haan). MSc dissertation, Ghent University.
80Zohdy, A.A.R., Eaton, G.P. & Mabey, D.R., 1974. Application of surface geophysics to ground-water investigations. Techniques of water-resources investigations of the USGS, Book 2, chapter D1.
81Manuscript received 22.09.2014, accepted in revised form 09.01.2015, available on line 27.01.2015. Modified version available on line 07.09.2015.